
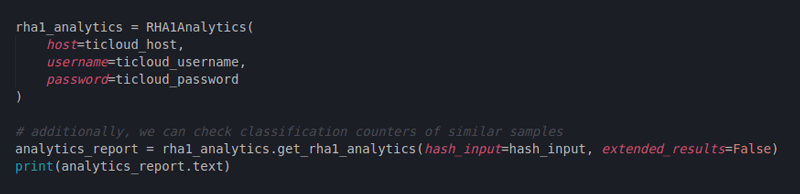
$$c = c_b (n_c \cdot n_d) [ (n_c \cdot n_d)^$ where $n'$ is on the order of $n^3$ (and, more crucially, where $1 < m < n$) such that $m^3$ is not reduced (and so you can just take cube roots). It can be used as a Python library as well as on the commandline. It supports encryption and decryption, signing and verifying signatures, and key generation according to PKCS1 version 1.5. 1 Answer Sorted by: 7 I guess you are refering to the case where three people have the following public keys : (n1, 3) ( n 1, 3), (n2, 3) ( n 2, 3) and (n3, 3) ( n 3, 3) (yes, e 3 e 3, and this attack is one of the reasons we don't use e 3 e 3 anymore).
Your problem can be fixed this way: decrypted rsakey.encrypt (rawcipherdata, 0) If the source really has encrypted with the private key, then theyve effectively signed the data. python3 rsa.py > openssl base64 -d -A > openssl rsautl -decrypt -inkey. The Wikipedia page has a nice explanation of the algorithm to find $c$. Python-RSA is a pure-Python RSA implementation. Public key is used to encrypt and private key is used to decrypt. genrsa -out cert.key Generating RSA private key, 1024 bit long modulus. You want to find:īecause $n_b$, $n_c$, $n_d$ are pairwise coprime (assume they have no common factors) a solution must exist. You know $m^3$ modulo each modulus, which is sufficient.


 0 kommentar(er)
0 kommentar(er)
